In "Failure is a feature in blameless DevOps," I discussed the central role of failure in delivering quality by soliciting feedback. This is the failure agile DevOps teams rely on to guide them and drive development. Test-driven development (TDD) is the conditio sine qua non of any agile DevOps value stream delivery. Failure-centric TDD methodology only works if it is paired with measurable tests.
TDD methodology is modeled on how nature works and how nature produces winners and losers in the evolutionary game.
Natural selection

In 1859, Charles Darwin proposed the theory of evolution in his book On the Origin of Species. Darwin's thesis was that natural variability is caused by the combination of spontaneous mutations in individual organisms and environmental pressures. These pressures eliminate less-adapted organisms while favoring other, more fit organisms. Each and every living being mutates its chromosomes, and those spontaneous mutations are carried to the next generation (the offspring). The newly emerged variability is then tested under natural selection—the environmental pressures that exist due to the variability of environmental conditions.
This simplified diagram illustrates the process of adjusting to environmental conditions.

Fig. 1. Different environmental pressures result in different outcomes governed by natural selection. Image screenshot from a video by Richard Dawkins.
This illustration shows a school of fish in their natural habitat. The habitat varies (darker or lighter gravel at the bottom of the sea or riverbed), as does each fish (darker or lighter body patterns and colors).
It also shows two situations (i.e., two variations of the environmental pressure):
- The predator is present
- The predator is absent
In the first situation, fish that are easier to spot against the gravel shade are at higher risk of being picked off by predators. When the gravel is darker, the lighter portion of the fish population is thinned out. And vice versa—when the gravel is a lighter shade, the darker portion of the fish population suffers the thinning out scenario.
In the second situation, fish are sufficiently relaxed to engage in mating. In the absence of predators and in the presence of the mating ritual, the opposite results can be expected: The fish that stand out against the background have a better chance of being picked for mating and transferring their characteristics to offspring.
Selection criteria
When selecting among variability, the process is never arbitrary, capricious, whimsical, nor random. The decisive factor is always measurable. That decisive factor is usually called a test or a goal.
A simple mathematical example can illustrate this process of decision making. (Only in this case it won't be governed by natural selection, but by artificial selection.) Suppose someone asks you to build a little function that will take a positive number and calculate that number's square root. How would you go about doing that?
The agile DevOps way is to fail fast. Start with humility, admitting upfront that you don't really know how to develop that function. All you know, at this point, is how to describe what you'd like to do. In technical parlance, you are ready to engage in crafting a unit test.
"Unit test" describes your specific expectation. It could simply be formulated as "given the number 16, I expect the square root function to return number 4." You probably know that the square root of 16 is 4. However, you don't know the square root for some larger numbers (such as 533).
At the very least, you have formulated your selection criteria, your test or goal.
Implement the failing test
The .NET Core platform can illustrate the implementation. .NET typically uses xUnit.net as a unit-testing framework. (To follow the coding examples, please install .NET Core and xUnit.net.)
Open the command line and create a folder where your square root solution will be implemented. For example, type:
mkdir square_rootThen type:
cd square_rootCreate a separate folder for unit tests:
mkdir unit_testsMove into the unit_tests folder (cd unit_tests) and initiate the xUnit framework:
dotnet new xunitNow, move one folder up to the square_root folder, and create the app folder:
mkdir app
cd appCreate the scaffold necessary for the C# code:
dotnet new classlibNow open your favorite editor and start cracking!
In your code editor, navigate to the unit_tests folder and open UnitTest1.cs.
Replace auto-generated code in UnitTest1.cs with:
using System;
using Xunit;
using app;
namespace unit_tests{
public class UnitTest1{
Calculator calculator = new Calculator();
[Fact]
public void GivenPositiveNumberCalculateSquareRoot(){
var expected = 4;
var actual = calculator.CalculateSquareRoot(16);
Assert.Equal(expected, actual);
}
}
}This unit test describes the expectation that the variable expected should be 4. The next line describes the actual value. It proposes to calculate the actual value by sending a message to the component called calculator. This component is described as capable of handling the CalculateSquareRoot message by accepting a numeric value. That component hasn't been developed yet. But it doesn't really matter, because this merely describes the expectations.
Finally, it describes what happens when the message is triggered to be sent. At that point, it asserts whether the expected value is equal to the actual value. If it is, the test passed and the goal is reached. If the expected value isn't equal to the actual value, the test fails.
Next, to implement the component called calculator, create a new file in the app folder and call it Calculator.cs. To implement a function that calculates the square root of a number, add the following code to this new file:
namespace app {
public class Calculator {
public double CalculateSquareRoot(double number) {
double bestGuess = number;
return bestGuess;
}
}
}Before you can test this implementation, you need to instruct the unit test how to find this new component (Calculator). Navigate to the unit_tests folder and open the unit_tests.csproj file. Add the following line in the <ItemGroup> code block:
<ProjectReference Include="../app/app.csproj" />Save the unit_test.csproj file. Now you are ready for your first test run.
Go to the command line and cd into the unit_tests folder. Run the following command:
dotnet testRunning the unit test will produce the following output:
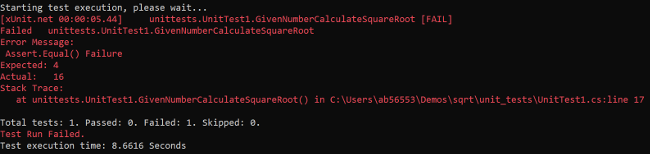
Fig. 2. xUnit output after the unit test run fails.
As you can see, the unit test failed. It expected that sending number 16 to the calculator component would result in the number 4 as the output, but the output (the actual value) was the number 16.
Congratulations! You have created your first failure. Your unit test provided strong, immediate feedback urging you to fix the failure.
Fix the failure
To fix the failure, you must improve bestGuess. Right now, bestGuess merely takes the number the function receives and returns it. Not good enough.
But how do you figure out a way to calculate the square root value? I have an idea—how about looking at how Mother Nature solves problems.
Emulate Mother Nature by iterating
It is extremely hard (pretty much impossible) to guess the correct value from the first (and only) attempt. You must allow for several attempts at guessing to increase your chances of solving the problem. And one way to allow for multiple attempts is to iterate.
To iterate, store the bestGuess value in the previousGuess variable, transform the bestGuess value, and compare the difference between the two values. If the difference is 0, you solved the problem. Otherwise, keep iterating.
Here is the body of the function that produces the correct value for the square root of any positive number:
double bestGuess = number;
double previousGuess;
do {
previousGuess = bestGuess;
bestGuess = (previousGuess + (number/previousGuess))/2;
} while((bestGuess - previousGuess) != 0);
return bestGuess;This loop (iteration) converges bestGuess values to the desired solution. Now your carefully crafted unit test passes!
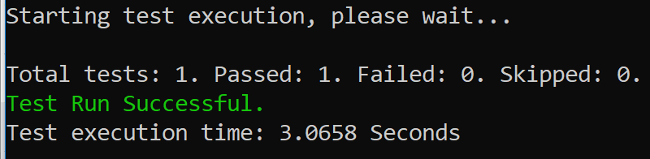
Fig. 3. Unit test successful, 0 tests failed.
The iteration solves the problem
Just like Mother Nature's approach, in this exercise, iteration solves the problem. An incremental approach combined with stepwise refinement is the guaranteed way to arrive at a satisfactory solution. The decisive factor in this game is having a measurable goal and test. Once you have that, you can keep iterating until you hit the mark.
Now the punchline!
OK, this was an amusing experiment, but the more interesting discovery comes from playing with this newly minted solution. Until now, your starting bestGuess was always equal to the number the function receives as the input parameter. What happens if you change the initial bestGuess?
To test that, you can run a few scenarios. First, observe the stepwise refinement as the iteration loops through a series of guesses as it tries to calculate the square root of 25:
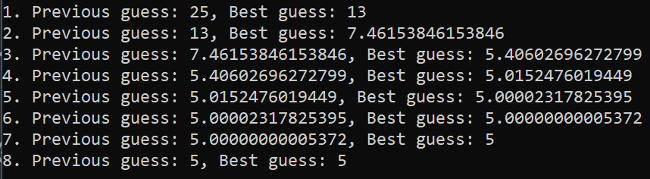
Fig. 4. Iterating to calculate the square root of 25.
Starting with 25 as the bestGuess, it takes eight iterations for the function to calculate the square root of 25. But what would happen if you made a comical, ridiculously wrong stab at the bestGuess? What if you started with a clueless second guess, that 1 million might be the square root of 25? What would happen in such an obviously erroneous situation? Would your function be able to deal with such idiocy?
Take a look at the horse's mouth. Rerun the scenario, this time starting from 1 million as the bestGuess:
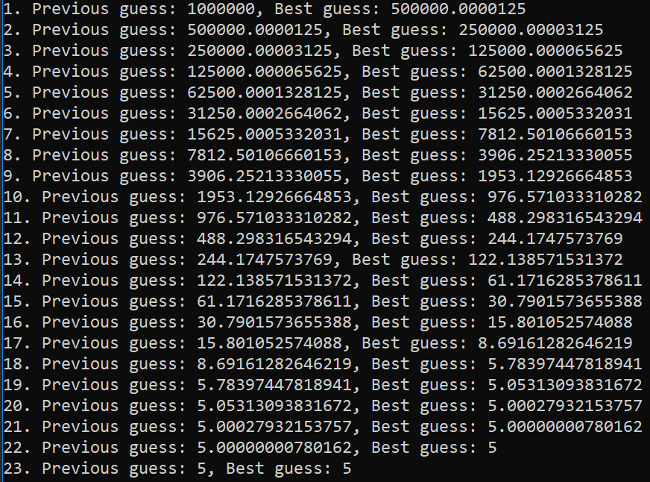
Fig. 5. Stepwise refinement when calculating the square root of 25 by starting with 1,000,000 as the initial bestGuess.
Oh wow! Starting with a ludicrously large number, the number of iterations only tripled (from eight iterations to 23). Not nearly as dramatic an increase as you might intuitively expect.
The moral of the story
The Aha! moment arrives when you realize that, not only is iteration guaranteed to solve the problem, but it doesn't matter whether your search for the solution begins with a good or a terribly botched initial guess. However erroneous your initial understanding, the process of iteration, coupled with a measurable test/goal, puts you on the right track and delivers the solution. Guaranteed.
Figures 4 and 5 show a steep and dramatic burndown. From a wildly incorrect starting point, the iteration quickly burns down to an absolutely correct solution.
This amazing methodology, in a nutshell, is the essence of agile DevOps.
Back to some high-level observations
Agile DevOps practice stems from the recognition that we live in a world that is fundamentally based on uncertainty, ambiguity, incompleteness, and a healthy dose of confusion. From the scientific/philosophical point of view, these traits are well documented and supported by Heisenberg's Uncertainty Principle (covering the uncertainty part), Wittgenstein's Tractatus Logico-Philosophicus (the ambiguity part), Gödel's incompleteness theorems (the incompleteness aspect), and the Second Law of Thermodynamics (the confusion caused by relentless entropy).
In a nutshell, no matter how hard you try, you can never get complete information when trying to solve any problem. It is, therefore, more profitable to abandon an arrogant stance and adopt a more humble approach to solving problems. Humility pays big dividends in rewarding you—not only with the hoped-for solution but also with the byproduct of a well-structured solution.
Conclusion
Nature works incessantly—it's a continuous flow. Nature has no master plan; everything happens as a response to what happened earlier. The feedback loops are very tight, and apparent progress/regress is piecemeal. Everywhere you look in nature, you see stepwise refinement, in one shape or form or another.
Agile DevOps is a very interesting outcome of the engineering model's gradual maturation. DevOps is based on the recognition that the information you have available is always incomplete, so you'd better proceed cautiously. Obtain a measurable test (e.g., a hypothesis, a measurable expectation), make a humble attempt at satisfying it, most likely fail, then collect the feedback, fix the failure, and continue. There is no plan other than agreeing that, with each step of the way, there must be a measurable hypothesis/test.
In the next article in this series, I'll take a closer look at how mutation testing provides much-needed feedback that drives value.






9 Comments