When Brendan Eich created JavaScript in 1995, he intended to do Scheme in the browser. Scheme, being a dialect of Lisp, is a functional programming language. Things changed when Eich was told that the new language should be the scripting language companion to Java. Eich eventually settled on a language that has a C-style syntax (as does Java), yet has first-class functions. Java technically did not have first-class functions until version 8, however you could simulate first-class functions using anonymous classes. Those first-class functions are what makes functional programming possible in JavaScript.
JavaScript is a multi-paradigm language that allows you to freely mix and match object-oriented, procedural, and functional paradigms. Recently there has been a growing trend toward functional programming. In frameworks such as Angular and React, you'll actually get a performance boost by using immutable data structures. Immutability is a core tenet of functional programming. It, along with pure functions, makes it easier to reason about and debug your programs. Replacing procedural loops with functions can increase the readability of your program and make it more elegant. Overall, there are many advantages to functional programming.
What functional programming isn't
Before we talk about what functional programming is, let's talk about what it is not. In fact, let's talk about all the language constructs you should throw out (goodbye, old friends):
- Loops
- while
- do...while
- for
- for...of
- for...in
- Variable declarations with var or let
- Void functions
- Object mutation (for example: o.x = 5;)
- Array mutator methods
- copyWithin
- fill
- pop
- push
- reverse
- shift
- sort
- splice
- unshift
- Map mutator methods
- clear
- delete
- set
- Set mutator methods
- add
- clear
- delete
How can you possibly program without those features? That's exactly what we are going to explore in the next few sections.
Pure functions
Just because your program contains functions does not necessarily mean that you are doing functional programming. Functional programming distinguishes between pure and impure functions. It encourages you to write pure functions. A pure function must satisfy both of the following properties:
- Referential transparency: The function always gives the same return value for the same arguments. This means that the function cannot depend on any mutable state.
- Side-effect free: The function cannot cause any side effects. Side effects may include I/O (e.g., writing to the console or a log file), modifying a mutable object, reassigning a variable, etc.
Let's illustrate with a few examples. First, the multiply function is an example of a pure function. It always returns the same output for the same input, and it causes no side effects.
The following are examples of impure functions. The canRide function depends on the captured heightRequirement variable. Captured variables do not necessarily make a function impure, but mutable (or re-assignable) ones do. In this case it was declared using let, which means that it can be reassigned. The multiply function is impure because it causes a side-effect by logging to the console.
The following list contains several built-in functions in JavaScript that are impure. Can you state which of the two properties each one does not satisfy?
- console.log
- element.addEventListener
- Math.random
- Date.now
- $.ajax (where $ == the Ajax library of your choice)
Living in a perfect world in which all our functions are pure would be nice, but as you can tell from the list above, any meaningful program will contain impure functions. Most of the time we will need to make an Ajax call, check the current date, or get a random number. A good rule of thumb is to follow the 80/20 rule: 80% of your functions should be pure, and the remaining 20%, of necessity, will be impure.
There are several benefits to pure functions:
- They're easier to reason about and debug because they don't depend on mutable state.
- The return value can be cached or "memoized" to avoid recomputing it in the future.
- They're easier to test because there are no dependencies (such as logging, Ajax, database, etc.) that need to be mocked.
If a function you're writing or using is void (i.e., it has no return value), that's a clue that it's impure. If the function has no return value, then either it's a no-op or it's causing some side effect. Along the same lines, if you call a function but do not use its return value, again, you're probably relying on it to do some side effect, and it is an impure function.
Immutability
Let's return to the concept of captured variables. Above, we looked at the canRide function. We decided that it is an impure function, because the heightRequirement could be reassigned. Here is a contrived example of how it can be reassigned with unpredictable results:
Let me reemphasize that captured variables do not necessarily make a function impure. We can rewrite the canRide function so that it is pure by simply changing how we declare the heightRequirement variable.
Declaring the variable with const means that there is no chance that it will be reassigned. If an attempt is made to reassign it, the runtime engine will throw an error; however, what if instead of a simple number we had an object that stored all our "constants"?
We used const so the variable cannot be reassigned, but there's still a problem. The object can be mutated. As the following code illustrates, to gain true immutability, you need to prevent the variable from being reassigned, and you also need immutable data structures. The JavaScript language provides us with the Object.freeze method to prevent an object from being mutated.
Immutability pertains to all data structures, which includes arrays, maps, and sets. That means that we cannot call mutator methods such as array.prototype.push because that modifies the existing array. Instead of pushing an item onto the existing array, we can create a new array with all the same items as the original array, plus the one additional item. In fact, every mutator method can be replaced by a function that returns a new array with the desired changes.
The same thing goes when using a Map or a Set. We can avoid mutator methods by returning a new Map or Set with the desired changes.
I would like to add that if you are using TypeScript (I am a huge fan of TypeScript), then you can use the Readonly<T>, ReadonlyArray<T>, ReadonlyMap<K, V>, and ReadonlySet<T> interfaces to get a compile-time error if you attempt to mutate any of those objects. If you call Object.freeze on an object literal or an array, then the compiler will automatically infer that it is read-only. Because of how Maps and Sets are represented internally, calling Object.freeze on those data structures does not work the same. But it's easy enough to tell the compiler that you would like them to be read-only.
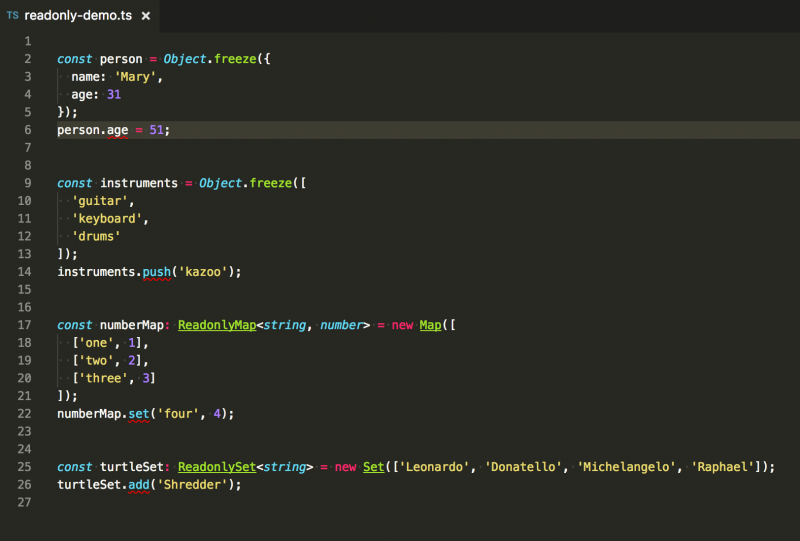
opensource.com
Okay, so we can create new objects instead of mutating existing ones, but won't that adversely affect performance? Yes, it can. Be sure to do performance testing in your own app. If you need a performance boost, then consider using Immutable.js. Immutable.js implements Lists, Stacks, Maps, Sets, and other data structures using persistent data structures. This is the same technique used internally by functional programming languages such as Clojure and Scala.
Function composition
Remember back in high school when you learned something that looked like (f ∘ g)(x)? Remember thinking, "When am I ever going to use this?" Well, now you are. Ready? f ∘ g is read "f composed with g." There are two equivalent ways of thinking of it, as illustrated by this identity: (f ∘ g)(x) = f(g(x)). You can either think of f ∘ g as a single function or as the result of calling function g and then taking its output and passing that to f. Notice that the functions get applied from right to left—that is, we execute g, followed by f.
A couple of important points about function composition:
- We can compose any number of functions (we're not limited to two).
- One way to compose functions is simply to take the output from one function and pass it to the next (i.e., f(g(x))).
There are libraries such as Ramda and lodash that provide a more elegant way of composing functions. Instead of simply passing the return value from one function to the next, we can treat function composition in the more mathematical sense. We can create a single composite function made up from the others (i.e., (f ∘ g)(x)).
Okay, so we can do function composition in JavaScript. What's the big deal? Well, if you're really onboard with functional programming, then ideally your entire program will be nothing but function composition. There will be no loops (for, for...of, for...in, while, do) in your code. None (period). But that's impossible, you say! Not so. That leads us to the next two topics: recursion and higher-order functions.
Recursion
Let's say that you would like to implement a function that computes the factorial of a number. Let's recall the definition of factorial from mathematics:
n! = n * (n-1) * (n-2) * ... * 1.
That is, n! is the product of all the integers from n down to 1. We can write a loop that computes that for us easily enough.
Notice that both product and i are repeatedly being reassigned inside the loop. This is a standard procedural approach to solving the problem. How would we solve it using a functional approach? We would need to eliminate the loop and make sure we have no variables being reassigned. Recursion is one of the most powerful tools in the functional programmer's toolbelt. Recursion asks us to break down the overall problem into sub-problems that resemble the overall problem.
Computing the factorial is a perfect example. To compute n!, we simply need to take n and multiply it by all the smaller integers. That's the same thing as saying:
n! = n * (n-1)!
A-ha! We found a sub-problem to solve (n-1)! and it resembles the overall problem n!. There's one more thing to take care of: the base case. The base case tells us when to stop the recursion. If we didn't have a base case, then recursion would go on forever. In practice, you'll get a stack overflow error if there are too many recursive calls.
What is the base case for the factorial function? At first you might think that it's when n == 1, but due to some complex math stuff, it's when n == 0. 0! is defined to be 1. With this information in mind, let's write a recursive factorial function.
Okay, so let's compute recursiveFactorial(20000), because... well, why not! When we do, we get this:
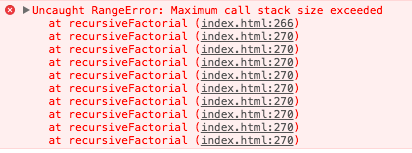
opensource.com
So what's going on here? We got a stack overflow error! It's not because of infinite recursion. We know that we handled the base case (i.e., n === 0). It's because the browser has a finite stack and we have exceeded it. Each call to recursiveFactorial causes a new frame to be put on the stack. We can visualize the stack as a set of boxes stacked on top of each other. Each time recursiveFactorial gets called, a new box is added to the top. The following diagram shows a stylized version of what the stack might look like when computing recursiveFactorial(3). Note that in a real stack, the frame on top would store the memory address of where it should return after executing, but I have chosen to depict the return value using the variable r. I did this because JavaScript developers don't normally need to think about memory addresses.

opensource.com
You can imagine that the stack for n = 20000 would be much higher. Is there anything we can do about that? It turns out that, yes, there is something we can do about it. As part of the ES2015 (aka ES6) specification, an optimization was added to address this issue. It's called the proper tail calls optimization (PTC). It allows the browser to elide, or omit, stack frames if the last thing that the recursive function does is call itself and return the result. Actually, the optimization works for mutually recursive functions as well, but for simplicity we're just going to focus on a single recursive function.
You'll notice in the stack above that after the recursive function call, there is still an additional computation to be made (i.e., n * r). That means that the browser cannot optimize it using PTC; however, we can rewrite the function in such a way so that the last step is the recursive call. One trick to doing that is to pass the intermediate result (in this case the product) into the function as an argument.
Let's visualize the optimized stack now when computing factorial(3). As the following diagram shows, in this case the stack never grows beyond two frames. The reason is that we are passing all necessary information (i.e., the product) into the recursive function. So, after the product has been updated, the browser can throw out that stack frame. You'll notice in this diagram that each time the top frame falls down and becomes the bottom frame, the previous bottom frame gets thrown out. It's no longer needed.
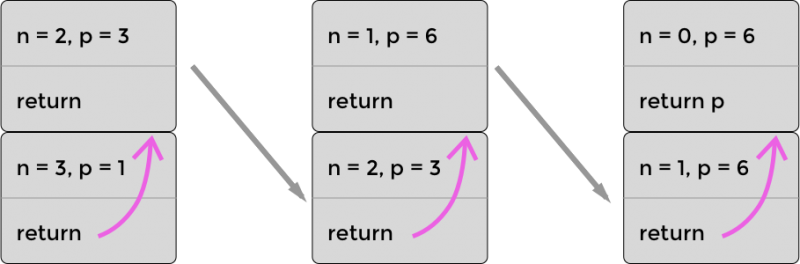
opensource.com
Now run that in a browser of your choice, and assuming that you ran it in Safari, then you will get the answer, which is Infinity (it's a number higher than the maximum representable number in JavaScript). But we didn't get a stack overflow error, so that's good! Now what about all the other browsers? It turns out that Safari is the only browser that has implemented PTC, and it might be the only browser to ever implement it. See the following compatibility table:

opensource.com
Other browsers have put forth a competing standard called syntactic tail calls (STC). "Syntactic" means that you will have to specify via new syntax that you would like the function to participate in the tail-call optimization. Even though there is not widespread browser support yet, it's still a good idea to write your recursive functions so that they are ready for tail-call optimization whenever (and however) it comes.
Higher-order functions
We already know that JavaScript has first-class functions that can be passed around just like any other value. So, it should come as no surprise that we can pass a function to another function. We can also return a function from a function. Voilà! We have higher-order functions. You're probably already familiar with several higher order functions that exist on the Array.prototype. For example, filter, map, and reduce, among others. One way to think of a higher-order function is: It's a function that accepts (what's typically called) a callback function. Let's see an example of using built-in higher-order functions:
Notice that we are calling methods on an array object, which is characteristic of object-oriented programming. If we wanted to make this a bit more representative of functional programming, we could use functions provided by Ramda or lodash/fp instead. We can also use function composition, which we explored in a previous section. Note that we would need to reverse the order of the functions if we use R.compose, since it applies the functions right to left (i.e., bottom to top); however, if we want to apply them left to right (i.e., top to bottom), as in the example above, then we can use R.pipe. Both examples are given below using Ramda. Note that Ramda has a mean function that can be used instead of reduce.
The advantage of the functional programming approach is that it clearly separates the data (i.e., vehicles) from the logic (i.e., the functions filter, map, and reduce). Contrast that with the object-oriented code that blends data and functions in the form of objects with methods.
Currying
Informally, currying is the process of taking a function that accepts n arguments and turning it into n functions that each accepts a single argument. The arity of a function is the number of arguments that it accepts. A function that accepts a single argument is unary, two arguments binary, three arguments ternary, and n arguments is n-ary. Therefore, we can define currying as the process of taking an n-ary function and turning it into n unary functions. Let's start with a simple example, a function that takes the dot product of two vectors. Recall from linear algebra that the dot product of two vectors [a, b, c] and [x, y, z] is equal to ax + by + cz.
The dot function is binary since it accepts two arguments; however, we can manually convert it into two unary functions, as the following code example shows. Notice how curriedDot is a unary function that accepts a vector and returns another unary function that then accepts the second vector.
Fortunately for us, we don't have to manually convert each one of our functions to a curried form. Libraries including Ramda and lodash have functions that will do it for us. In fact, they do a hybrid type of currying, where you can either call the function one argument at a time, or you can continue to pass in all the arguments at once, just like the original.
Both Ramda and lodash also allow you to "skip over" an argument and specify it later. They do this using a placeholder. Because taking the dot product is commutative, it won't make a difference in which order we passed the vectors into the function. Let's use a different example to illustrate using a placeholder. Ramda uses a double underscore as its placeholder.
One final point before we complete the topic of currying, and that is partial application. Partial application and currying often go hand in hand, though they really are separate concepts. A curried function is still a curried function even if it hasn't been given any arguments. Partial application, on the other hand, is when a function has been given some, but not all, of its arguments. Currying is often used to do partial application, but it's not the only way.
The JavaScript language has a built-in mechanism for doing partial application without currying. This is done using the function.prototype.bind method. One idiosyncrasy of this method is that it requires you to pass in the value of this as the first argument. If you're not doing object-oriented programming, then you can effectively ignore this by passing in null.
Wrapping up
I hope you enjoyed exploring functional programming in JavaScript with me! For some it may be a completely new programming paradigm, but I hope you will give it a chance. I think you'll find that your programs are easier to read and debug. Immutability will also allow you to take advantage of performance optimizations in Angular and React.
This article is based on Matt's OpenWest talk, JavaScript the Good-er Parts. OpenWest will be held July 12-15, 2017 in Salt Lake City, Utah.







2 Comments