What the pandas Python data analysis library and SQL taught me about taking an average

For Python developers who work primarily with data, it's hard not to find yourself constantly knee-deep in SQL and Python's open source data library, pandas. Despite how easy these tools have made it to manipulate and transform data—sometimes as concisely as one line of code—analysts still must always understand their data and what their code means. Even calculating something as simple as summary statistics can be prone to serious mistakes.

In this article, we take a look at the arithmetic mean. Although it is conventionally taught with one-dimensional data in mind, calculating it for multidimensional data requires a fundamentally different process. In fact, calculating the arithmetic mean as if your data is one-dimensional will produce grossly incorrect figures, sometimes orders of magnitude off from what was intended. For me, this was a humbling experience: Even the arithmetic mean is no less deserving of double- and triple-checking than any other calculation.

Few statistical calculations rival the simplicity and explanatory power of the most basic: percentage, sum, and average, above all. As a result, they crop up everywhere, from exploratory data analysis to data dashboards and management reports. But one of these, the arithmetic mean, is unusually problematic. Although it is conventionally taught with one-dimensional data in mind, calculating it for multidimensional data requires a fundamentally different process. In fact, calculating the arithmetic mean as if your data is one-dimensional will produce grossly incorrect figures, sometimes orders of magnitude off from what was intended. For me, this was a humbling experience: Even the arithmetic mean is no less deserving of double- and triple-checking than any other calculation.

Back to basics

The arithmetic mean is defined as:

Image by:

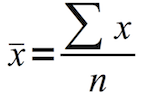
opensource.com

Or:

SUM(all observations) / COUNT(number of observations)

We can see this through a simple apple-picking example:

Apples

name	num_apples
Katie	4
Alan	8
John	10
Tess	8
Jessica	5

What composes an observation here? One individual, defined by a single column (name), also known as a dimension or attribute.

Using the formula above, we can calculate the arithmetic mean:

SUM(4 + 8 + 10 + 8 + 5) / 5 = 7

In SQL, we would write:

SELECT AVG(num_apples) FROM apples

What did we just calculate? "The average number of apples picked by person" (where each person represents one observation).

Adding complexity: Two-dimensional data

Apples

date	name	num_apples
2017-09-24	Katie	4
2017-09-24	Alan	8
2017-09-24	John	10
2017-09-24	Tess	8
2017-09-26	Katie	5

In this example, we replaced Jessica with Katie, but on a different date.

Now each observation in the table is not simply (name). Katie appears twice, but on separate observations because Katie picked apples on two different days. Rather, each observation is composed of two dimensions: (date, name).

We can ask the same question as before: "What is the average number of apples picked by person?"

We should expect a single number, just like before. Should we expect the average to equal 7, like we got before?

Going back to our formula:

Image by:

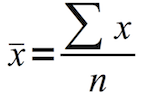
opensource.com

Or:

SUM(4 + 8 + 10 + 8 + 5) / 4 = 8.75

So although the numerator (number of apples picked) has stayed the same, the denominator (number of people) went from 5 to 4. Katie picked apples twice, on separate days, so we don't double count her.

What's going on here? The unit of observation defined at the table level differs from the unit of observation for our analysis.

For our analytical question, we are not asking about how many days everyone picked apples. We're simply asking for the average number of apples picked by everybody, and we should end up with an answer like "7 apples picked on average" or "10 apples picked on average." If Katie happens to pick apples on more days than everyone else, that should genuinely increase the average. In any random sample of apple pickers, we may get people like Katie who pick apples much more often than anyone else, which pushes up the average number of apples picked by person.

So how would we write this in SQL? This would not work:

SELECT AVG(num_apples) FROM apples

This would give us the same answer as before: 7.

What we have to do is collapse the data to the level of analysis we care about. We aren't asking for the average number of apples picked by date-person, which is what the query before would give us. We are asking about the number of apples the average person picks. The level of observation for our analysis is a person (name), not a date-person (date, name).

So our query would look like this:

SELECT AVG(num_apples) FROM (
    SELECT name, SUM(num_apples) AS num_apples
    FROM apples
    GROUP BY name
) AS t

Scary.

The inner query gives us this result set:

Apples

name	num_apples
Katie	9
Alan	8
John	10
Tess	8

Now, that's what we want to take the average of! The outer query then does this:

SUM(4 + 8 + 10 + 8 + 5) / 4 = 8.75

So what did we learn here? Our analytical question required that we reduce the dimensionality of the data to less than what was defined by the table. The table defined an observation of two dimensions (date, name), but our analytical question demanded an observation of one dimension (name).

This change in dimensionality via collapsing resulted in a change in the amount of observations in the denominator, which changed our average.

And to restate the obvious: if we didn't perform this collapsing operation on our original data, the first average we calculated would be wrong.

Why does this happen, more generally?

When data is stored in a database, a level of granularity must be specified. In other words, "what constitutes an individual observation?"

You could imagine a table storing data like this:

Sales

date	products_sold
2017-09-21	21
2017-09-22	28
2017-09-24	19
2017-09-25	21
2017-09-26	19
2017-09-27	18

But you could also imagine a table that stores the same data but just with more granularity, like this:

Sales

date	product_category	products_sold
2017-09-21	T-Shirts	16
2017-09-21	Jackets	2
2017-09-21	Hats	3
2017-09-22	T-Shirts	23
2017-09-22	Hats	5
2017-09-24	T-Shirts	10
2017-09-24	Jackets	3
2017-09-24	Hats	6
2017-09-25	T-Shirts	21
2017-09-26	T-Shirts	14
2017-09-26	Hats	5
2017-09-27	T-Shirts	14
2017-09-27	Jackets	4

The unit of observation defined at the table-level is called the primary key. A primary key is required in all database tables and applies a constraint that every observation must be unique. After all, if an observation appears twice but isn't unique, it should just be one observation. 

It typically follows a syntax like this:

CREATE TABLE sales (
    date DATE NOT NULL default '0000-00-00',
    product_category VARCHAR(40) NOT NULL default '',
    products_sold INT
    PRIMARY KEY (date, product_category) <------
)

Notice that the level of granularity we choose to record about our data is literally part of the definition of our table. The primary key defines "a single observation" in our data. And it's required before we start storing any data at all.

Now, just because we record data at that level of granularity doesn't mean we need to analyze it at that level of granularity. The level of granularity at which we need to analyze our data will always be a function of what kind of questions we are trying to answer.

The key takeaway here is that the primary key defines an observation at the table level, and this may comprise one or two or 20 dimensions. But our analysis will probably not define an observation so granularly (e.g., we may care just about sales per day), so we must collapse the data and redefine the observation for our analysis.

Formalizing the pattern

So we know that, for any analytical question we ask, we need to redefine what constitutes a single observation, independent of whatever the primary key happens to be. If we just take the average without collapsing our data, we will end up with too many observations (i.e., the amount defined by the primary key) in our denominator, and therefore too low an average.

To review, using the same data as above:

Sales

date	product_category	products_sold
2017-09-21	T-Shirts	16
2017-09-21	Jackets	2
2017-09-21	Hats	3
2017-09-22	T-Shirts	23
2017-09-22	Hats	5
2017-09-24	T-Shirts	10
2017-09-24	Jackets	3
2017-09-24	Hats	6
2017-09-25	T-Shirts	21
2017-09-26	T-Shirts	14
2017-09-26	Hats	5
2017-09-27	T-Shirts	14
2017-09-27	Jackets	4

"What's the average number products sold per day?"

Well, there are six days in this data set and a total of 126 products sold. That's 21 products sold per day on average.

It is not 9.7, which is what you get from this query:

SELECT AVG(products_sold) FROM sales

We need to collapse the data like so:

SELECT AVG(quantity) FROM (
    SELECT date, SUM(products_sold) AS quantity
    FROM sales
    GROUP BY date
) AS t

Giving us 21. We can get a sense of the magnitude here: 9.7 is not at all close to 21.

Annotating that query above:

SELECT AVG(quantity) FROM (
    SELECT date, SUM(products_sold) AS quantity
    FROM sales
    GROUP BY date // [COLLAPSING KEY]
) AS t

Here, I define the collapsing key as the "unit of observation relevant to our analysis." It has nothing to do with the primary key—it ignores any columns we don't care about, such as (product_category). The collapsing key says: "We want to work only this level of granularity, so roll up any granularity below by adding it all up."

In this case, we are explicitly defining a unit of observation for our analysis as (date), which will compose the number of rows in the denominator. If we don't do this, who knows how many observations (rows) will slip into the denominator? (Answer: However many we see at the primary key level.)

Unfortunately, the collapsing key is not the end of the story.

What if we want averages for groups? Like, "What's the average number of products sold by category?"

Working with groups

"What's the average number of products sold by category?"

Seems like a harmless question. What could go wrong?

SELECT product_category, AVG(products_sold)
FROM sales
GROUP BY product_category

Nothing. That actually works. That's the right answer. We get:

Sales

product_category	AVG(products_sold)
T-Shirts	12.83
Jackets	3
Hats	4.75

Sanity checking for jackets: There are three days where we sell jackets, and we sell a total 4 + 3 + 2 = 9, so the average is 3.

Immediately I'm thinking: "Three what?" Answer: "Three jackets sold on average." Question: "Average what?" Answer: "On an average day, we sell three jackets."

OK, now we see our original question wasn't precise enough—it said nothing about days!

Here's the question we really answered: "For each product category, what's the average number of products sold per day?"

Anatomy of an averaging question, in English

Since the goal of any SQL query is to ultimately be a direct, declarative translation of a question posed in plain English, we first need to understand the parts of the question in English.

Let's decompose this: "For each product category, what's the average number of products sold per day?"

There are three parts:

• Groups: We want an average for each product category (product_category)
• Observation: Our denominator should be the number of days (date)
• Measurement: The numerator is the measurement variable we are summing up (products_sold)

For each group, we want an average, which will be the total number of products sold per day divided by the number of days in that group.

Our goal is to translate these English components directly into SQL.

From English to SQL

Here is some transaction data:

Transactions

date	product	state	purchaser	quantity
2016-12-23	vacuum	NY	Brian King	1
2016-12-23	stapler	NY	Brian King	3
2016-12-23	printer ink	NY	Brian King	2
2016-12-23	stapler	NY	Trevor Campbell	1
2016-12-23	vacuum	MA	Lauren Mills	1
2016-12-23	printer ink	MA	John Smith	5
2016-12-24	vacuum	MA	Lauren Mills	1
2016-12-24	keyboard	NY	Brian King	2
2016-12-25	keyboard	MA	Tom Lewis	4
2016-12-26	stapler	NY	John Doe	1

"For each state and product, what's the average number of products sold per day?"

SELECT state, product, AVG(quantity)
FROM transactions
GROUP BY state, product

This gives us:

Transactions

state	product	AVG(quantity)
NY	vacuum	1
NY	stapler	1.66
NY	printer ink	2
NY	keyboard	2
MA	vacuum	1
MA	printer ink	5
MA	keyboard	4

Sanity checking on (NY, stapler), we should get a total of 3 + 1 + 1 = 5 over 2 days (2017-12-23 and 2017-12-26), giving us 2.5...

Alas, the SQL result gives us 1.66. The query must be wrong.

Here's the right query:

SELECT state, product, AVG(quantity) FROM (
    SELECT state, product, date, SUM(quantity) as quantity
    FROM transactions
    GROUP BY state, product, date
) AS t
GROUP BY state, product

Giving us:

Transactions

state	product	AVG(quantity)
NY	vacuum	1
NY	stapler	2.5
NY	printer ink	2
NY	keyboard	2
MA	vacuum	1
MA	printer ink	5
MA	keyboard	4

Anatomy of an averaging question, in SQL

We determined that there are three parts to an averaging question in English, and if we don't respect that, we're going to miscalculate the average. We also know that the components in English should translate into components in SQL. 

Here they are:

SELECT state, product, 
AVG(quantity) // [MEASUREMENT VARIABLE]
FROM (
    SELECT state, product, date, SUM(quantity) as quantity
    FROM transactions
    GROUP BY state, product, date // [COLLAPSING KEY]
) AS t
GROUP BY state, product // [GROUPING KEY]

    -- [OBSERVATION KEY] = [COLLAPSING KEY] - [GROUPING KEY]
    -- (date) = (state, product, date) - (state, product)

This is the same query as above, just with comments.

Notice that the collapsing key is not in our English question—it's like faking a primary key, but for our analysis instead of using the one defined in the table. 

Also notice that in the SQL translation, the observation key is implicit, not explicit. The observation key is equal to the collapsing key (i.e., just the dimensions we need for our analysis, and nothing more) minus the grouping key (the dimensions on which we're grouping). Whatever's left—that's the observation key, or what defines an observation for our analysis.

I am the first to admit just how confusing it is that the most important part of our averaging question—that is, what defines an observation—is not even explicit in SQL. It is implicit. I call this the pitfall of taking multidimensional averages.

The takeaway is as follows:

• The collapsing key defines what dimensions we will use in our analysis. Everything else from the primary key of the table is to be "rolled up." We define the collapsing key in the GROUP BY of the inner query.
• The grouping key is upon what dimension we want to group our data (i.e., "for each group"). This is defined in the GROUP BY of the outer query.
• The collapsing key − the grouping key = the observation key.
• If you don't define a collapsing key, you are implicitly using the primary key of the table as your collapsing key.
• If you aren't doing any grouping, the collapsing key equals the observation key

By way of example, if the primary key of your table is (date, product, state, purchaser) and you want to take an average by purchaser (observation: purchaser) for each state (group: state), you have to solve for the collapsing key (i.e., what goes in the inner SQL query).

We don't want to implicitly use the primary key, so we're going to use a collapsing key. What collapsing key? The collapsing key will be (observation key: purchaser) + (grouping key: state) = (purchaser, state). That goes in the GROUP BY of our inner query, (state) alone goes in GROUP BY of the outer query, and implicitly the observation key is (purchaser).

Finally, notice what happens if we don't use a collapsing key. The primary key is (date, product, state, purchaser) and our grouping key is (state). If we don't use any subqueries at all, we will get an answer which defines an observation as (date, product, state, purchaser) − (state) = (date, product, purchaser). And that will determine how many observations we see in each group, which affects the denominator of our average. Which is wrong.

Wrapping up

One thing I've learned from all of this is, from an analytical point of view, never trust the primary key. It defines the granularity—i.e., what constitutes an observation—for recording data, but this may not be what you need for analysis. And if you aren't expressly aware of how this difference will affect your calculations, your calculations may very well be incorrect. Because the primary key will affect your denominator whether you are aware or not.

So if you can't trust the primary key, the safest thing to do is to always collapse the data. If you aren't doing any grouping, then your collapsing key explicitly equals your observation key. If you are doing grouping, then your collapsing key is the sum of your observation and grouping keys. But one thing's for sure: If you are not collapsing your data, you are implicitly trusting the primary key.

The second thing I learned is that, totally unrelated to SQL, asking a question about an average is not always intuitive. "What is the average share price by security by day?" is an ambiguous question, even in plain English! Is that an average share price by day for each security, or an average share by security for each day?

Business questions don't come in the form of database logic or program code. Rather, they are formulated using natural language and must be translated into data language. As a data analyst, you must clarify: "What exactly are we taking the average of?" Here it's helpful to think in terms of collapsing, grouping, and observation keys, especially when conceptualizing how many observations are going into your denominator.

This problem isn't confined to SQL, but rather any store of relational data, such as pandas.DataFrames or R data tables. And if you're anything like me, you'll go poring over your old code grepping for averages and wonder, "just what exactly am I averaging here?"

This was originally published on alexpetralia.com and is reprinted with permission.

To learn more, attend Alex Petralia's talk, Analyzing data: What pandas and SQL taught me about taking an average, at PyCon Cleveland 2018.