From 2014 and 2017, I had the good fortune of working with a multidisciplinary team in Chile, building decision support tools to facilitate the planning of hydroelectric capacity as an alternative to fossil-fuel based thermoelectric capacity. Our job was also to aid in the design of transmission line corridors. Transmission lines carry “bulk electricity” from where the electricity is generated to where it is consumed. Those lines are strung from towers that are placed within transmission corridors, where vegetation and access are managed for safety. In many countries, the location of these corridors is carefully planned in order to take into account engineering feasibility as well as social, cultural, environmental and other economic factors.
Earlier, I wrote about the hydroelectric capacity planning exercise, but the transmission corridor planning projects came along later, and in the context of those projects, we learned more about the valuation framework we used and about how open source software provided great solutions for scenario generation and testing and general trade-off analysis. I’ll revisit those details here.
Objects of value
Fundamental to both hydroelectric capacity and transmission corridor planning is some way of characterizing the importance, or value, of existing landscape features. For our studies, we adapted and extended the six High Conservation Values defined by the HCV Network (species diversity, landscape level ecosystems, ecosystems and habitats, ecosystem services, community needs, and cultural values).
In the case of hydroelectric capacity, we defined specific groups of objects of value related to fluvial ecosystems, terrestrial ecosystems, social concerns related to rural subsistence, indigenous cultural concerns, non-indigenous cultural concerns, and other economic uses of the land.
In the case of transmission corridor planning, we were able to omit fluvial ecosystem concerns as, generally speaking, transmission lines tend to cross fluvial networks without significant impact.
One of the reasons for this adaptation and extension was in recognition of the kinds of supporting data generally available in Chile. Much of this data is available in the form of shapefiles, a commonly-used data format for geospatial data. In this way, we were able to leverage existing databases that either directly described our objects of value (for example, national parks), or provided a proxy (for example, locations of indigenous communities served as one of the proxies for areas of interest to indigenous people), or modeled such an object (for example, models that predicted presence of species at risk based on measured local factors).
In the case of fluvial ecosystems, our team found it necessary to manually classify stream reaches according to their natural characteristics and the presence of a built environment in their vicinity.
We were able to leverage a number of open source geospatial tools, such as QGIS, GDAL/OGR, and the PostGIS extension to the PostgreSQL open source relational database, in order to control the quality of the geospatial data at hand. These tools also helped us carry out the types of spatial analysis necessary to determine relationships between the various objects of value and, on the one hand, the potential hydropower projects, and on the other, the possible alternative transmission corridors.
Hydroelectric capacity planning
The key to hydroelectric capacity planning in Chile is the ability to generate the maximum amount of electricity, given certain restrictions, while assuring a fixed level of interaction with objects of value.
This is a variation of the classic 0-1 Knapsack Problem, where the goal is to fill a limited-capacity knapsack with the most valuable objects chosen from a large collection. We found that, when we sorted the potential hydroelectric projects in decreasing order of hydroelectric potential and plotted hydroelectric potential and “other value” as determined by the presence of objects of value, we always saw a distribution similar to:
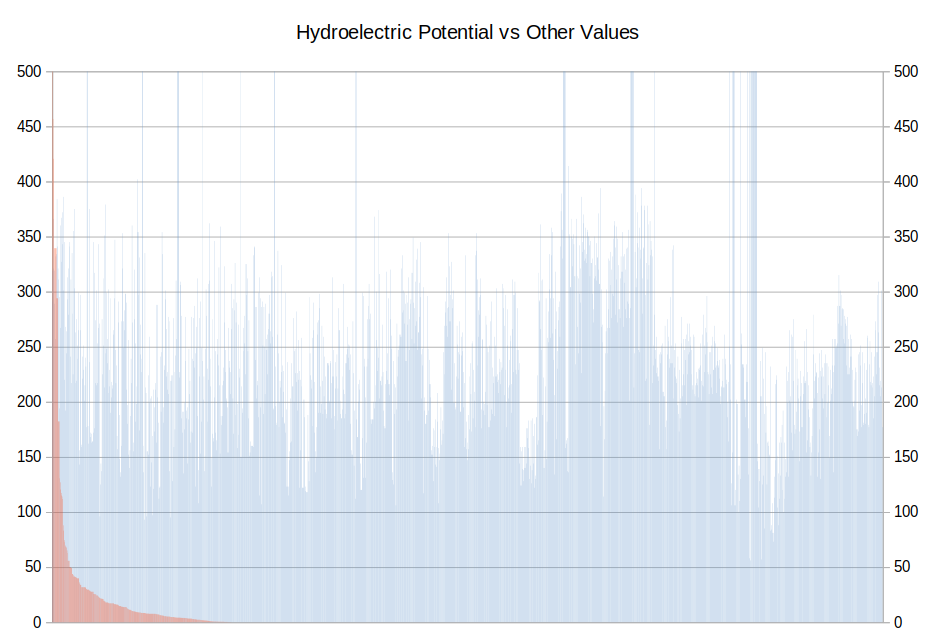
The hydroelectric potential can be seen as the monotonically decreasing bars in red; the other values as the “picket fence” in blue. The large blue bars disappearing off the top of the chart indicate the presence of national parks, where no development is permitted.
Note: All of the graphs I needed, including the one above, I created with LibreOffice Calc.
This type of correlation between hydroelectric potential and other values, or rather, the lack of it, tells us that we should be able to optimize for power production from a very limited number of sites; and that is, in fact, what we found.
The wonderful Rosetta Code site offered numerous means of solving the 0-1 Knapsack Problem. Because I’m a huge fan of the Groovy programming language, and because the dynamic programming solution presented in Groovy on that page is so compact and elegant, I chose that to use as the basis for a tool to evaluate scenarios. In our case, the “weight” of the projects is defined as the sum of their objects of value, and the “value” is defined as the hydroelectric potential. Of course, we could have formulated this problem to select projects that picked potential projects in order to minimize their interaction with objects of value; however, the relative independence of hydroelectric potential and other values suggested that this formulation would not be as appropriate.
It’s worth noting that the “obvious” interpretation of “impact” on objects of value is not completely appropriate; in some cases, hydroelectric development doesn’t affect objects of value; and in others, hydroelectric development may even enhance local economic, social and cultural development, by being forced to create conservation plans that are harmonious with development. What we did observe was that a high total value for objects of value predicted with reasonable accuracy the amount of dialogue and planning necessary to arrive at a mutually acceptable solution.
Transmission corridor planning
The key to transmission corridor planning in Chile is to recognize that building a transmission line involves a great deal of negotiation with stakeholders along the way, and therefore one possible approach is to choose a corridor that minimizes the amount of negotiation – in essence, choose a least-cost path for the corridor, using the total of objects of value as a measure of cost.
Finding least-cost pathways has been an area of study since at least the mid 20th century. E.W. Dijkstra is credited with the most famous solution to the shortest path problem. Since then, numerous methods have been developed that provide faster solutions.
In our case, we represented the problem as a two-dimensional raster with the cost of moving from one cell of the raster to another given by the cost of entering that new cell, as defined by the total of the objects of value interacting with that new cell. We converted this conceptual model into a directed graph. Because we weren’t looking for “THE shortest path”, but rather a number of alternative solutions, we broke the search in two – finding the shortest path from each of two points (the start and end point of the line to be designed) to all other points in the “feasible area”. Using that, we could show the areas in which transmission corridors could be developed that would need less than a certain level of interaction. In an area we selected for proof of concept of the methodology, these areas of similar cost looked like:
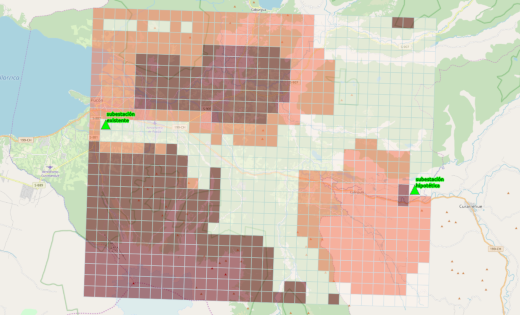
The areas in which transmission corridors could be developed that would need less than a certain level of interaction. Via QGIS and OpenStreetMap
The areas of “harder to traverse” appear in dark reddish-brown; those “easier to traverse” are in pale orange-pink; and those “easiest to traverse” are very pale yellow-white.
With this kind of “cost of traversal surface”, we identified an initial broad corridor in which more detailed studies can be carried out in order to support the determination of a final and precise corridor. That corridor appears in pale green in the image below:
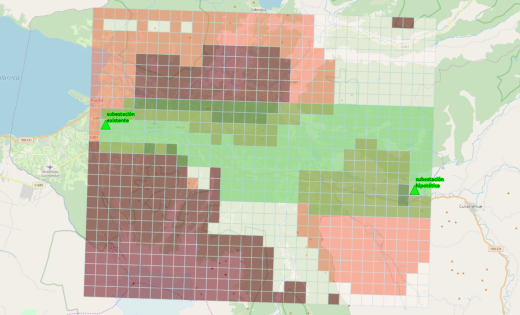
In pale green, an initial broad corridor in which more detailed studies can be carried out in order to support the determination of a final and precise corridor. Via QGIS and OpenStreetMap
Note that this broad corridor incorporates a small amount of the harder-to-traverse and easier-to-traverse areas because the western extent of the easiest-to-traverse portion of the image is so narrow.
Again, open source came to the rescue, in this case in the form of a variant of Dijkstra’s algorithm called “K-Shortest Paths” as implemented in Java by Yan Qi at Arizona State University. I chose this Java version partly because of the great interoperability between Java and Groovy, which I was again using for all the data management work.
Concluding comments
Are there other ways to solve these problems? Most assuredly.
Recently I played around with using the Julia programming language to handle the 0-1 Knapsack problem. And of course there are shortest path algorithms implemented in both open source and “other” geographic information systems. But for me, in the end, the cool thing has been the ability to rely on the work of others, and to offer our work in return, to solve these kinds of problems. And, dare I say, doing a small bit to saving the planet.






Comments are closed.