Many of us use password managers to securely store our many unique passwords. A critical part of a password manager is the master password. This password protects all others, and in that way, it is a risk. Anyone who has it can pretend to be you… anywhere! Naturally, you keep your master password hard to guess, commit it to memory, and do all the other things you are supposed to do.
But what if something happens and you forget it? Maybe you took a vacation to a lovely, far-away island with no technology for a month. After frolicking in the water daily and eating pineapples, you cannot quite remember your password. Maybe it was "long legs travel fast"? Or was it something like "sharp spoons eat quick"? It was definitely clever when you thought of it.
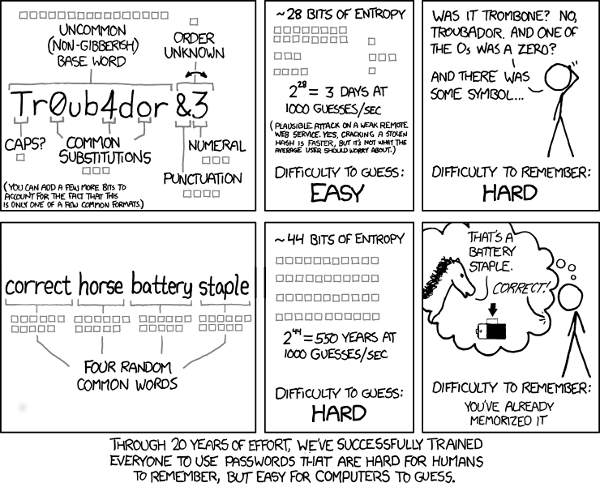
(XKCD, CC BY-NC 2.5)
Of course, you never told a single soul your password. Why, this is literally the first rule of password management. What could you have done differently?
Enter Shamir's Secret Sharing, an algorithm that allows users to divide a secret into parts that can be used only in combination with the other pieces.
Let's take a look at Shamir's Secret Sharing in action through a story of ancient times and modern times.
This story does assume some knowledge of cryptography. You can brush up on it with this introduction to cryptography and public key infrastructure.
A story of secrets in ancient times
In an ancient kingdom, it came to pass that the king had a secret. A terrible secret:
def int_from_bytes(s):
acc = 0
for b in s:
acc = acc * 256
acc += b
return acc
secret = int_from_bytes("terrible secret".encode("utf-8"))So terrible, the king could entrust it to none of his offspring. He had five of them but knew that there would be dangers on the road ahead. The king knew his children would need the secret to protect the kingdom after his death, but he could not bear the thought of the secret being known for two decades, while they were still mourning him.
So he used powerful magic to split the secret into five shards. He knew that it was possible that one child or even two would not respect his wishes, but he did not believe three of them would:
from mod import Mod
from os import urandomThe king was well-versed in the magical arts of finite fields and randomness. As a wise king, he used Python to split the secret.
The first thing he did was choose a large prime—the 13th Mersenne Prime (2**521 - 1)—and ordered it be written in letters 10 feet high, wrought of gold, above the palace:
P = 2**521 - 1This was not part of the secret: it was public data.
The king knew that if P is a prime, numbers modulo P form a mathematical field: they can be added, multiplied, subtracted, and divided as long as the divisor is not zero.
As a busy king, he used the PyPI package mod, which implements modulus arithmetic.
He made sure his terrible secret was less than P:
secret < PTRUEAnd he converted it to its modulus mod P:
secret = mod.Mod(secret, P)In order to allow three offspring to reconstruct the secret, the king had to generate two more parts to mix together:
polynomial = [secret]
for i in range(2):
polynomial.append(Mod(int_from_bytes(urandom(16)), P))
len(polynomial)3The king next needed to evaluate this polynomial at random points. Evaluating a polynomial is calculating polynomial[0] + polynomial[1]*x + polynomial[2]*x**2 ...
While there are third-party modules to evaluate polynomials, they do not work with finite fields. The king needed to write the evaluation code himself:
def evaluate(coefficients, x):
acc = 0
power = 1
for c in coefficients:
acc += c * power
power *= x
return accNext, the king evaluated the polynomial at five different points, to give one piece to each offspring:
shards = {}
for i in range(5):
x = Mod(int_from_bytes(urandom(16)), P)
y = evaluate(polynomial, x)
shards[i] = (x, y)Sadly, as the king feared, not all his offspring were honest and true. Two of them, shortly after his death, tried to figure out the terrible secret from the parts they had. Try as they could, they did not succeed. However, when the others learned this, they exiled them from the kingdom forever:
del shards[2]
del shards[3]Twenty years later, as the king had decreed, the oldest sibling and the two youngest came together to figure out their father's terrible secret. They put together their shards:
retrieved = list(shards.values())For 40 days and 40 nights, they struggled with finding the king's secret. No easy task was it before them. Like the king, they knew Python, but none were as wise as he.
Finally, the answer came to them.
The retrieval code is based on a concept called lagrange interpolation. It evaluates a polynomial at 0 based on its values in n other places, where n is the degree of the polynomial. The way it works is that you can explicitly find a formula for a polynomial that is 1 at t[0] and 0 at t[i] for i different from 0. Since evaluating a polynomial is a linear function, you evaluate each of these polynomials and interpolate the results of the evaluations with the values the polynomial has:
from functools import reduce
from operator import mul
def retrieve_original(secrets):
x_s = [s[0] for s in secrets]
acc = Mod(0, P)
for i in range(len(secrets)):
others = list(x_s)
cur = others.pop(i)
factor = Mod(1, P)
for el in others:
factor *= el * (el - cur).inverse()
acc += factor * secrets[i][1]
return accIt is no surprise this took them 40 days and 40 nights—this code is pretty complicated! But they ran it on the surviving shards, waiting with bated breath:
retrieved_secret = retrieve_original(retrieved)Did the children get the correct secret?
retrieved_secret == secretTRUEThe beauty of math's magic is that it works reliably every time! The children, now older and able to understand their father's choices, used the terrible secret to defend the kingdom. The kingdom prospered and grew.
A modern story of Shamir's Secret Sharing
In modern times, many of us are also burdened with a terrible secret: the master password to our password manager. While few people have one person they can trust completely with their deepest, darkest secrets, many can find a group of five where it is unlikely three will break their trust together.
Luckily, in these modern times, we do not need to split our secrets ourselves, as the king did. Through the modern technology of open source, we can use software that exists.
Let's say you have five people you trust—not absolutely, but quite a bit: Your best friend, your spouse, your mom, a close colleague, and your lawyer.
You can install and run the program ssss to split the key:
$ echo 'long legs travel fast' | ssss-split -t 3 -n 5
Generating shares using a (3,5) scheme with dynamic security level.
Enter the secret, at most 128 ASCII characters: Using a 168 bit security level.
1-797842b76d80771f04972feb31c66f3927e7183609
2-947925f2fbc23dc9bca950ef613da7a4e42dc1c296
3-14647bdfc4e6596e0dbb0aa6ab839b195c9d15906d
4-97c77a805cd3d3a30bff7841f3158ea841cd41a611
5-17da24ad63f7b704baed220839abb215f97d95f4f8Ah, a strong, powerful, master password: long legs travel fast. Never can it be entrusted to a single soul, but you can send the five shards to your five guardians.
- You send
1to your best friend, F. - You send
2to your spouse, S. - You send
3to your mom, M. - You send
4to your colleague, C. - You send
5to your lawyer, L.
Now, say you go on a family vacation. For a month, you frolic on the warm sands of the beach. While you frolic, you touch not one electronic device. Soon enough, your powerful master password is forgotten.
Your loving spouse and your dear mother were with you on vacation. They kept their shards safe in their password manager—and they have forgotten their passwords.
This is fine.
You contact your best friend, F, who gives you 1-797842b76d80771f04972feb31c66f3927e7183609. Your colleague, who covered all your shifts, is glad to have you back and gives you 4-97c77a805cd3d3a30bff7841f3158ea841cd41a611. Your lawyer charges you $150 per hour, goes into their password manager, and digs up 5-17da24ad63f7b704baed220839abb215f97d95f4f8.
With those three pieces, you run:
$ ssss-combine -t 3
Enter 3 shares separated by newlines:
Share [1/3]: 1-797842b76d80771f04972feb31c66f3927e7183609
Share [2/3]: 4-97c77a805cd3d3a30bff7841f3158ea841cd41a611
Share [3/3]: 5-17da24ad63f7b704baed220839abb215f97d95f4f8
Resulting secret: long legs travel fastAnd so, with the technology of open source, you too can live like a king!
Share safely for your safety
Password management is an essential skill for today's online life. Create a complex password, of course, but don't stop there. Use the handy Shamir's Secret Sharing algorithm to safely share it with others.










11 Comments