The GNU Image Manipulation Program (GIMP) is my go-to solution for image editing. Its toolset is very powerful and convenient, except for doing fractals, which is one thing you cannot draw by hand easily. These are fascinating mathematical constructs that have the characteristic of being self-similar. In other words, if they are magnified in some areas, they will look remarkably similar to the unmagnified picture. Besides being interesting, they also make very pretty pictures!

Rotated and magnified portion of the Mandelbrot set using Firecode. (Cristiano Fontana, CC BY-SA 4.0)
GIMP can be automated with Script-Fu to do batch processing of images or create complicated procedures that are not practical to do by hand; drawing fractals falls in the latter category. This tutorial will show how to draw a representation of the Mandelbrot fractal using GIMP and Script-Fu.

Mandelbrot set drawn with a colored environment using GIMP's Firecode palette. (Cristiano Fontana, CC BY-SA 4.0)

Rotated and magnified portion of the Mandelbrot set using Firecode. (Cristiano Fontana, CC BY-SA 4.0)
In this tutorial, you will write a script that creates a layer in an image and draws a representation of the Mandelbrot set with a colored environment around it.
What is the Mandelbrot set?
Do not panic! I will not go into too much detail here. For the more math-savvy, the Mandelbrot set is defined as the set of complex numbers a for which the succession
zn+1 = zn2 + a
does not diverge when starting from z₀ = 0.
In reality, the Mandelbrot set is the fancy-looking black blob in the pictures; the nice-looking colors are outside the set. They represent how many iterations are required for the magnitude of the succession of numbers to pass a threshold value. In other words, the color scale shows how many steps are required for the succession to pass an upper-limit value.
GIMP's Script-Fu
Script-Fu is the scripting language built into GIMP. It is an implementation of the Scheme programming language.
If you want to get more acquainted with Scheme, GIMP's documentation offers an in-depth tutorial. I also wrote an article about batch processing images using Script-Fu. Finally, the Help menu offers a Procedure Browser with very extensive documentation with all of Script-Fu's functions described in detail.
(Cristiano Fontana, CC BY-SA 4.0)
Scheme is a Lisp-like language, so a major characteristic is that it uses a prefix notation and a lot of parentheses. Functions and operators are applied to a list of operands by prefixing them:
(function-name operand operand ...)
(+ 2 3)
↳ Returns 5
(list 1 2 3 5)
↳ Returns a list containing 1, 2, 3, and 5Write the script
You can write your first script and save it to the Scripts folder found in the preferences window under Folders → Scripts. Mine is at $HOME/.config/GIMP/2.10/scripts. Write a file called mandelbrot.scm with:
; Complex numbers implementation
(define (make-rectangular x y) (cons x y))
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (magnitude z)
(let ((x (real-part z))
(y (imag-part z)))
(sqrt (+ (* x x) (* y y)))))
(define (add-c a b)
(make-rectangular (+ (real-part a) (real-part b))
(+ (imag-part a) (imag-part b))))
(define (mul-c a b)
(let ((ax (real-part a))
(ay (imag-part a))
(bx (real-part b))
(by (imag-part b)))
(make-rectangular (- (* ax bx) (* ay by))
(+ (* ax by) (* ay bx)))))
; Definition of the function creating the layer and drawing the fractal
(define (script-fu-mandelbrot image palette-name threshold domain-width domain-height offset-x offset-y)
(define num-colors (car (gimp-palette-get-info palette-name)))
(define colors (cadr (gimp-palette-get-colors palette-name)))
(define width (car (gimp-image-width image)))
(define height (car (gimp-image-height image)))
(define new-layer (car (gimp-layer-new image
width height
RGB-IMAGE
"Mandelbrot layer"
100
LAYER-MODE-NORMAL)))
(gimp-image-add-layer image new-layer 0)
(define drawable new-layer)
(define bytes-per-pixel (car (gimp-drawable-bpp drawable)))
; Fractal drawing section.
; Code from: https://rosettacode.org/wiki/Mandelbrot_set#Racket
(define (iterations a z i)
(let ((z′ (add-c (mul-c z z) a)))
(if (or (= i num-colors) (> (magnitude z′) threshold))
i
(iterations a z′ (+ i 1)))))
(define (iter->color i)
(if (>= i num-colors)
(list->vector '(0 0 0))
(list->vector (vector-ref colors i))))
(define z0 (make-rectangular 0 0))
(define (loop x end-x y end-y)
(let* ((real-x (- (* domain-width (/ x width)) offset-x))
(real-y (- (* domain-height (/ y height)) offset-y))
(a (make-rectangular real-x real-y))
(i (iterations a z0 0))
(color (iter->color i)))
(cond ((and (< x end-x) (< y end-y)) (gimp-drawable-set-pixel drawable x y bytes-per-pixel color)
(loop (+ x 1) end-x y end-y))
((and (>= x end-x) (< y end-y)) (gimp-progress-update (/ y end-y))
(loop 0 end-x (+ y 1) end-y)))))
(loop 0 width 0 height)
; These functions refresh the GIMP UI, otherwise the modified pixels would be evident
(gimp-drawable-update drawable 0 0 width height)
(gimp-displays-flush)
)
(script-fu-register
"script-fu-mandelbrot" ; Function name
"Create a Mandelbrot layer" ; Menu label
; Description
"Draws a Mandelbrot fractal on a new layer. For the coloring it uses the palette identified by the name provided as a string. The image boundaries are defined by its domain width and height, which correspond to the image width and height respectively. Finally the image is offset in order to center the desired feature."
"Cristiano Fontana" ; Author
"2021, C.Fontana. GNU GPL v. 3" ; Copyright
"27th Jan. 2021" ; Creation date
"RGB" ; Image type that the script works on
;Parameter Displayed Default
;type label values
SF-IMAGE "Image" 0
SF-STRING "Color palette name" "Firecode"
SF-ADJUSTMENT "Threshold value" '(4 0 10 0.01 0.1 2 0)
SF-ADJUSTMENT "Domain width" '(3 0 10 0.1 1 4 0)
SF-ADJUSTMENT "Domain height" '(3 0 10 0.1 1 4 0)
SF-ADJUSTMENT "X offset" '(2.25 -20 20 0.1 1 4 0)
SF-ADJUSTMENT "Y offset" '(1.50 -20 20 0.1 1 4 0)
)
(script-fu-menu-register "script-fu-mandelbrot" "<Image>/Layer/")I will go through the script to show you what it does.
Get ready to draw the fractal
Since this image is all about complex numbers, I wrote a quick and dirty implementation of complex numbers in Script-Fu. I defined the complex numbers as pairs of real numbers. Then I added the few functions needed for the script. I used Racket's documentation as inspiration for function names and roles:
(define (make-rectangular x y) (cons x y))
(define (real-part z) (car z))
(define (imag-part z) (cdr z))
(define (magnitude z)
(let ((x (real-part z))
(y (imag-part z)))
(sqrt (+ (* x x) (* y y)))))
(define (add-c a b)
(make-rectangular (+ (real-part a) (real-part b))
(+ (imag-part a) (imag-part b))))
(define (mul-c a b)
(let ((ax (real-part a))
(ay (imag-part a))
(bx (real-part b))
(by (imag-part b)))
(make-rectangular (- (* ax bx) (* ay by))
(+ (* ax by) (* ay bx)))))Draw the fractal
The new function is called script-fu-mandelbrot. The best practice for writing a new function is to call it script-fu-something so that it can be identified in the Procedure Browser easily. The function requires a few parameters: an image to which it will add a layer with the fractal, the palette-name identifying the color palette to be used, the threshold value to stop the iteration, the domain-width and domain-height that identify the image boundaries, and the offset-x and offset-y to center the image to the desired feature. The script also needs some other parameters that it can deduce from the GIMP interface:
(define (script-fu-mandelbrot image palette-name threshold domain-width domain-height offset-x offset-y)
(define num-colors (car (gimp-palette-get-info palette-name)))
(define colors (cadr (gimp-palette-get-colors palette-name)))
(define width (car (gimp-image-width image)))
(define height (car (gimp-image-height image)))
...Then it creates a new layer and identifies it as the script's drawable. A "drawable" is the element you want to draw on:
(define new-layer (car (gimp-layer-new image
width height
RGB-IMAGE
"Mandelbrot layer"
100
LAYER-MODE-NORMAL)))
(gimp-image-add-layer image new-layer 0)
(define drawable new-layer)
(define bytes-per-pixel (car (gimp-drawable-bpp drawable)))For the code determining the pixels' color, I used the Racket example on the Rosetta Code website. It is not the most optimized algorithm, but it is simple to understand. Even a non-mathematician like me can understand it. The iterations function determines how many steps the succession requires to pass the threshold value. To cap the iterations, I am using the number of colors in the palette. In other words, if the threshold is too high or the succession does not grow, the calculation stops at the num-colors value. The iter->color function transforms the number of iterations into a color using the provided palette. If the iteration number is equal to num-colors, it uses black because this means that the succession is probably bound and that pixel is in the Mandelbrot set:
; Fractal drawing section.
; Code from: https://rosettacode.org/wiki/Mandelbrot_set#Racket
(define (iterations a z i)
(let ((z′ (add-c (mul-c z z) a)))
(if (or (= i num-colors) (> (magnitude z′) threshold))
i
(iterations a z′ (+ i 1)))))
(define (iter->color i)
(if (>= i num-colors)
(list->vector '(0 0 0))
(list->vector (vector-ref colors i))))Because I have the feeling that Scheme users do not like to use loops, I implemented the function looping over the pixels as a recursive function. The loop function reads the starting coordinates and their upper boundaries. At each pixel, it defines some temporary variables with the let* function: real-x and real-y are the real coordinates of the pixel in the complex plane, according to the parameters; the a variable is the starting point for the succession; the i is the number of iterations; and finally color is the pixel color. Each pixel is colored with the gimp-drawable-set-pixel function that is an internal GIMP procedure. The peculiarity is that it is not undoable, and it does not trigger the image to refresh. Therefore, the image will not be updated during the operation. To play nice with the user, at the end of each row of pixels, it calls the gimp-progress-update function, which updates a progress bar in the user interface:
(define z0 (make-rectangular 0 0))
(define (loop x end-x y end-y)
(let* ((real-x (- (* domain-width (/ x width)) offset-x))
(real-y (- (* domain-height (/ y height)) offset-y))
(a (make-rectangular real-x real-y))
(i (iterations a z0 0))
(color (iter->color i)))
(cond ((and (< x end-x) (< y end-y)) (gimp-drawable-set-pixel drawable x y bytes-per-pixel color)
(loop (+ x 1) end-x y end-y))
((and (>= x end-x) (< y end-y)) (gimp-progress-update (/ y end-y))
(loop 0 end-x (+ y 1) end-y)))))
(loop 0 width 0 height)At the calculation's end, the function needs to inform GIMP that it modified the drawable, and it should refresh the interface because the image is not "automagically" updated during the script's execution:
(gimp-drawable-update drawable 0 0 width height)
(gimp-displays-flush)Interact with the user interface
To use the script-fu-mandelbrot function in the graphical user interface (GUI), the script needs to inform GIMP. The script-fu-register function informs GIMP about the parameters required by the script and provides some documentation:
(script-fu-register
"script-fu-mandelbrot" ; Function name
"Create a Mandelbrot layer" ; Menu label
; Description
"Draws a Mandelbrot fractal on a new layer. For the coloring it uses the palette identified by the name provided as a string. The image boundaries are defined by its domain width and height, which correspond to the image width and height respectively. Finally the image is offset in order to center the desired feature."
"Cristiano Fontana" ; Author
"2021, C.Fontana. GNU GPL v. 3" ; Copyright
"27th Jan. 2021" ; Creation date
"RGB" ; Image type that the script works on
;Parameter Displayed Default
;type label values
SF-IMAGE "Image" 0
SF-STRING "Color palette name" "Firecode"
SF-ADJUSTMENT "Threshold value" '(4 0 10 0.01 0.1 2 0)
SF-ADJUSTMENT "Domain width" '(3 0 10 0.1 1 4 0)
SF-ADJUSTMENT "Domain height" '(3 0 10 0.1 1 4 0)
SF-ADJUSTMENT "X offset" '(2.25 -20 20 0.1 1 4 0)
SF-ADJUSTMENT "Y offset" '(1.50 -20 20 0.1 1 4 0)
)Then the script tells GIMP to put the new function in the Layer menu with the label "Create a Mandelbrot layer":
(script-fu-menu-register "script-fu-mandelbrot" "<Image>/Layer/")Having registered the function, you can visualize it in the Procedure Browser.
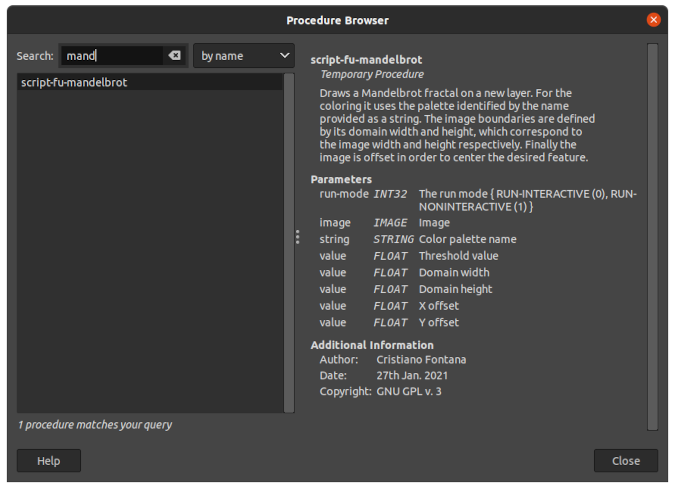
Procedure Browser with script-fu-mandelbrot function. (Cristiano Fontana, CC BY-SA 4.0)
Run the script
Now that the function is ready and registered, you can draw the Mandelbrot fractal! First, create a square image and run the script from the Layers menu.
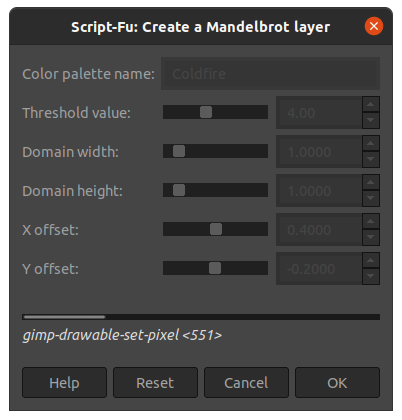
(Cristiano Fontana, CC BY-SA 4.0)
The default values are a good starting set to obtain the following image. The first time you run the script, create a very small image (e.g., 60x60 pixels) because this implementation is slow! It took several hours for my computer to create the following image in full 1920x1920 pixels. As I mentioned earlier, this is not the most optimized algorithm; rather, it was the easiest for me to understand.

Mandelbrot set drawn with a colored environment using GIMP's Firecode palette. (Cristiano Fontana, CC BY-SA 4.0)
Learn more
This tutorial showed how to use GIMP's built-in scripting features to draw an image created with an algorithm. These images show GIMP's powerful set of tools that can be used for artistic applications and mathematical images.
If you want to move forward, I suggest you look at the official documentation and its tutorial. As an exercise, try modifying this script to draw a Julia set, and please share the resulting image in the comments.










Comments are closed.